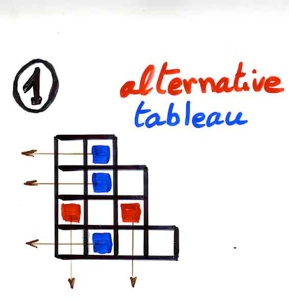
First, I shall introduce a new combinatorial object called "alternative tableau". It is defined as a Ferrers diagram (or Young diagram) where some cells are colored blue or red, satisfying the following condition (Ferrers diagram are drawn in the french way):

    there are no colored cells located at the left of (resp. below) a blue (resp. red) cell.

Let  n  be the total number of rows and columns of the Ferrers diagram (some rows or columns may be empty), then the number of alternative tableaux of size n  is equal to (n+1)! .

             

                                       

          

                                     

  

An alternative tableau of size 8

I shall give a direct bijection, called the “exchange-deletion algorithm” between permutations and alternative tableaux. A variation of the algorithm, called “exchange-fusion algorithm” will be useful for the study of properties of that bijection. Particular case includes interpretation of the Genocchi numbers and classification of permutations according to the so-called “Genocchi shape”.

      

 

             The “exchange-delete” algorithm:

a bijection between permutations and alternative tableaux

The purpose of this survey talk, is to show how I came to the notion of alternative tableaux and how I discovered the bijection with permutations.

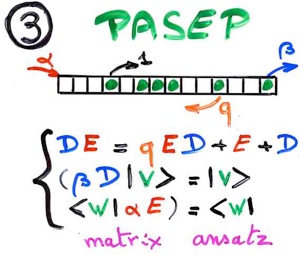
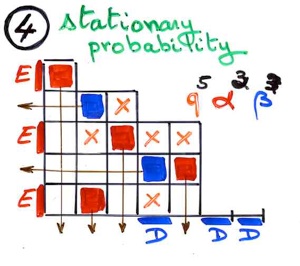
The model PASEP (partially asymmetric exclusion process) is a toy model in the physics of dynamical systems far from equilibrium. It is a model of particles with mutual exclusion, hoping left or right in a finite strip of cells, with entries at each sides of the strip. There are some probabilities parameters to get in or out at both sides, and also to hop right or left inside the strip. There exists a system of stationary probabilities distribution among the 2^n possibles states. The model is simple enough to allow explicit resolution, but have transition phases and can be used as realistic modelisation (molecular diffusion, traffic flow, etc ...). It has been intensively studied by physicists, especially with the seminal paper of Derrida, Evans, Hakim, Pasquier (1993) giving the stationary probabilities in term of a “matrix ansatz”.

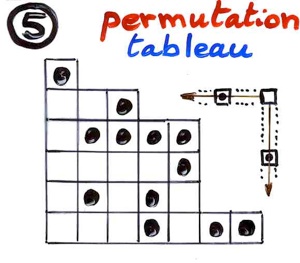
The model PASEP has been recently intensively studied by combinatorists, in particular giving combinatorial interpretations of the stationary distribution (works of  Brak, Corteel, Essam, Parvianinen, Rechnitzer, Williams, Duchi, Schaeffer, Viennot, ...). Some interpretations are in term of the so-called "permutation tableaux", introduced by Postnikov, followed by Steingrimsson and Williams, in relation with some considerations in algebraic geometry (total positivity on the Grassmannian).

In fact, contrary to other studies of the PASEP by combinatorists, the matrix ansatz of Derrida and his coauthors, with the commutation relation between operators D and E  satisfying 

DE = qED + E + D, 

is the starting point of our combinatorial considerations. Considering the operators D and E as formal variables, they generate a quadratic algebra. Computations can be made by considering the rewritings rules “DE gives ED or E or D”. Introducing a “planarisation” of these rewritings rules, leads to the notion of alternative tableaux and an interpretation of the stationary probabilities of the PASEP in term of alternative tableaux.

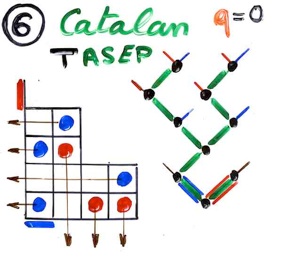
Permutations tableaux have been studied by Postnikov, Steingrimsson, Williams, Burstein, Corteel, Nadeau, in relation with the subject of forbidden patterns in permutations, and various bijections with permutations have been given. The advantage of introducing alternative tableaux is to give a complete symmetric role for rows and columns. We give a bijection between the two kinds of tableaux. The case of the TASEP (totally asymmetric exclusion process), i.e. when particles moves only in one direction, is interpreted by “Catalan alternative tableaux”. Such tableaux are enumerated by Catalan numbers and bijection with binary trees can be given. This corresponds to the case q = 0.

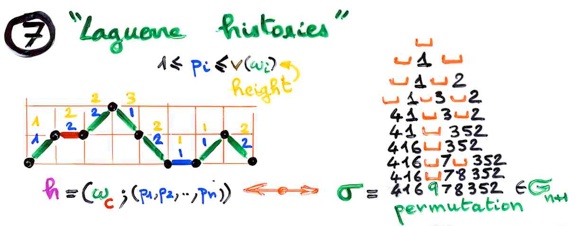
Then, in order to explain how I came to the “exchange-deletion” bijection between alternative tableaux and permutations, I need two ingredients from combinatorics: the so-called “Laguerre histories” and the interpretation by S.Fomin of the RSK  (Robinson-Schensted-Knuth) correspondence with “local rules”.

First, I shall recall the “FV” bijection (given with  J.Françon in 1978) between permutations and “Laguerre histories”  (i.e.  certain colored Motzkin paths, with some weight for each elementary steps). This bijection is at the heart of the combinatorial theory of orthogonal polynomials (or continued fractions) developed by P. Flajolet and the author in the 80’s.

The construction of a permutation from the Laguerre history enable us to give a “combinatorial representation” of operators D and E satisfying the commutation relation DE = ED + E + D.

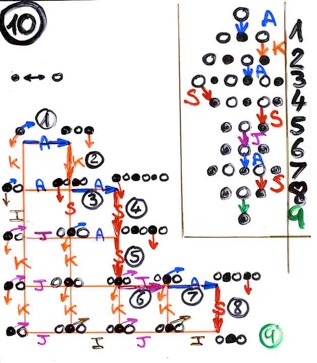
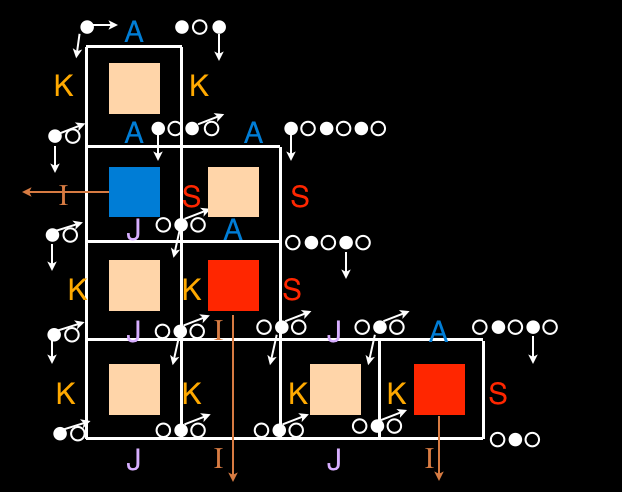
In fact we will introduce four combinatorial operators A, S, J, K, acting on what we call alternative words, with  D = A+ J  and  E = S + K. These  operators are inspired from Françon’s theory of “data histories” (1978) (in french: “histoires de fichiers”). So we will make a detour in data structures and the theory of integrated cost of data structures developed by Flajolet, Françon, Vuillemin. The four above operators A, S, J, K correspond to the possible primitive operations in the “dictionary” data structure.

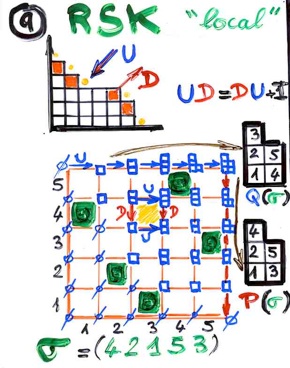
Then, we will recall the classical RSK correspondence between permutations and pair of standard Young tableaux of the same shape, the Schützenberger “jeu de taquin”, and a beautiful alternative definition of  RSK by S.Fomin, based on “local rules” coming in fact from a combinatorial interpretation of operators U and D satisfying the Heisenberg commutation relation  UD = DU + I .

We will show, by applying the same idea as in RSK, to the operators A, S, J, K, leads us to a certain bijection  between Laguerre histories and alternative tableaux. This bijection is defined by certain “local rules” expressing the combinatorial interpretation on alternative words of the commutation rules satisfied by the operators A, S, J, K. In fact our bijection between Laguerre histories and alternative tableaux would be an analog of the bijection (extension of RSK) between “oscillating tableaux” and involutions with no fixed points. Taking the inverse of  the permutations in bijection with Laguerre histories, we redefined this RSK- like bijection by a kind of algorithm having the flavor of Schützenberger’s jeu de taquin. This last algorithm is nothing but the “exchange-deletion” algorithm given at the beginning of the talk.

   

 

Some perspectives include hopes for a combinatorial theory of Askey-Wilson polynomials and an alternative study for alternating sign matrices and FPL using an analogous algebraic approach with operators and commutations rules. (see the talk at ESI, Vienna, 20 May 2008).

notes: The “exchange-fusion” algorithm and the detour with Françon’s theory of data histories was not explained in the talk at the Newton Institute, but will be in the complementary set of slides.